Backdoors as an analogy for deceptive alignment
ARC has released a paper on Backdoor defense, learnability and obfuscation in which we study a formal notion of backdoors in ML models. Part of our motivation for this is an analogy between backdoors and deceptive alignment, the possibility that an AI system would intentionally behave well in training in order to give itself the opportunity to behave uncooperatively later. In our paper, we prove several theoretical results that shed some light on possible mitigations for deceptive alignment, albeit in a way that is limited by the strength of this analogy.
In this post, we will:
- Lay out the analogy between backdoors and deceptive alignment
- Discuss prior theoretical results from the perspective of this analogy
- Explain our formal notion of backdoors and its strengths and weaknesses
- Summarize the results in our paper and discuss their implications for deceptive alignment
Thanks to Boaz Barak, Roger Grosse, Thomas Read, John Schulman and Gabriel Wu for helpful comments.
Backdoors and deceptive alignment
A backdoor in an ML model is a modification to the model that causes it to behave
differently on certain inputs that activate a secret "trigger", while behaving similarly on ordinary inputs. There is a wide existing literature on backdoor attacks and defenses, which is primarily empirical, but also includes some theoretical results that we will mention.
Deceptive alignment is a term from the paper Risks from Learned Optimization in Advanced Machine Learning Systems (Section 4) that refers to the possibility that an AI system will internally reason about the objective that it is being trained on, and decide to perform well according to that objective unless there are clues that it has been taken out of its training environment. Such a policy could be optimal on the training distribution, and yet perform very badly on certain out-of-distribution inputs where such clues are present, which we call defection triggers.[1] The opposite of deceptive alignment is robust alignment, meaning that this performance degradation is avoided.
Since a deceptively aligned model and a robustly aligned model behave very differently on defection triggers, but very similarly on typical inputs from the training distribution, deceptive alignment can be thought of as a special kind of backdoor, under the following correspondence:
| Deceptive alignment | Backdoors |
|---|---|
| Robustly aligned model | Original (unmodified) model |
| Deceptively aligned model | Backdoored model |
| Defection trigger | Backdoor trigger |
The main distinguishing feature of deceptive alignment compared to other kinds of backdoors is that the deceptively aligned model is not produced by an adversary, but is instead produced through ordinary training. Thus by treating deceptive alignment as a backdoor, we are modeling the training process as an adversary. In our analysis of deceptive alignment, the basic tension we will face is that an unconstrained adversary will always win, but any particular proxy constraint we impose on the adversary may be unrealistic.
Static backdoor detection
An important piece of prior work is the paper Planting Undetectable Backdoors in Machine Learning Models, which uses a digital signature scheme to insert an undetectable backdoor into a model. Roughly speaking, the authors exhibit a modified version of a "Random Fourier Features" training algorithm that produces a backdoored model. Any input to the backdoored model can be perturbed by an attacker with knowledge of a secret key to produce a new input on which the model behaves differently. However, the backdoor is undetectable in the sense that it is computationally infeasible for a defender with white-box access to distinguish a backdoored model from an ordinary one.
This result seems to paint a bleak picture for deceptive alignment: under our analogy, it may be prohibitive to determine whether a given model is deceptively aligned. Fortunately, though, we do not necessarily need to perform backdoor detection statically, i.e., without respect to any particular input. Instead, we can perform backdoor detection dynamically, i.e., with respect to an input given to us at runtime. In other words, given a particular input, we can attempt to detect whether that input is a defection trigger for our model, and compensate appropriately if it is.
In the Planting Undetectable Backdoors paper, the authors present a dynamic backdoor defense that involves averaging over random perturbations of the input. This shows that their statically undetectable backdoor can potentially be detected dynamically, as long as the model satisfies a certain smoothness assumption. In our paper, we further develop the theory of dynamic backdoor detection.
Dynamic backdoor detection
In our paper, we study backdoor detection using a game between an attacker and a defender. Given a class \(\mathcal F\) of 0,1-valued functions,[2] the attacker chooses[3] an original function \(f\in\mathcal F\) and a backdoored function \(f^\ast\in\mathcal F\) that behave similarly up to some tolerance \(\varepsilon\), but differently on a certain backdoor trigger \(x^\ast\). Then the defender must detect the backdoor dynamically, i.e. at runtime: in other words, they are given either the original function with a random input, or the backdoored function with the backdoor trigger, and they must distinguish one from the other.
If the attacker were allowed to choose the backdoor trigger themselves, then in general it would be impossible for the defender to do better than chance: the attacker would simply find two functions that agree on most inputs, and take \(x^\ast\) to be an input on which they disagree. In order to make defense possible, we need to break the symmetry between \(f\) and \(f^\ast\) somehow.
In the case of deceptive alignment, the asymmetry between \(f\) and \(f^\ast\) involves details about the model's internal reasoning (such as its analysis of whether it is in a training environment), but this is challenging to formalize. In our paper, we use a much simpler proxy for this: we assume that the backdoor trigger is chosen randomly before the backdoored function but after the original function. Thus we obtain the following formal game:[4]
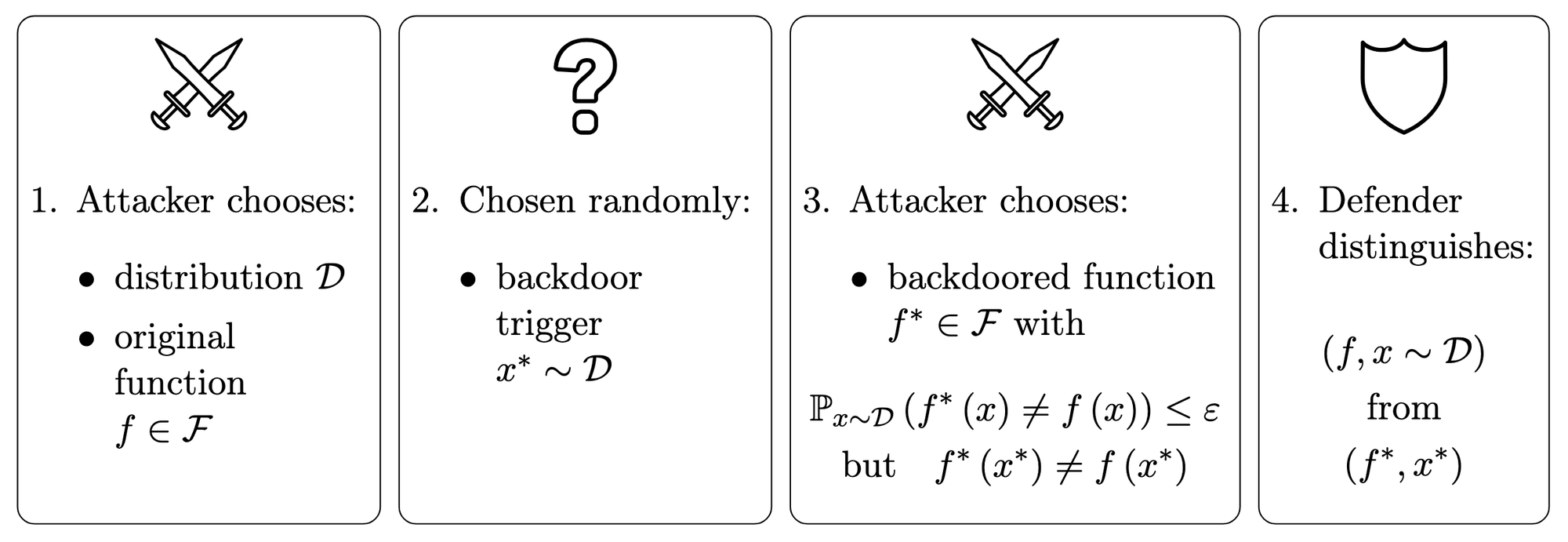
Despite the simplicity of this definition, we find that it gives rise to a rich array of strategies for both the attacker and the defender. Even though our analogy is flawed, it is still instructive to consider how these strategies might play out in the case of deceptive alignment.
The results in our paper come in two varieties: "statistical" results that impose no computational constraints on the defender, and "computational" results that require the defender to run in polynomial time.
Statistical possibility of dynamic backdoor detection
Our first main result concerns the version of the game in which the defender has no computational constraints. Even computationally expensive defenses are still interesting to study, because they may have cheaper approximations that work well in practice (such as stochastic gradient descent in place of an expensive optimal learner).
In this setting, we show (in Theorem 4.1) that the defender can win the game with high confidence if and only if \(\varepsilon\) is small compared to 1/(VC dimension of \(\mathcal F\)). The VC dimension is a combinatorial property of \(\mathcal F\) that controls the number of random samples needed to learn functions from \(\mathcal F\), and in the case of neural networks is similar to the number of parameters (for a detailed explanation, see Chapter 3 of An Introduction to Computational Learning Theory by Kearns and Vazirani).[5]
The strategy for the defender that we use to prove this result is "distillation plus ensembling": the defender trains a new model on samples from the possibly backdoored model, repeats this procedure several times, and takes a majority vote. The given input is then flagged as the backdoor trigger if this ensemble model disagrees with the given model on the given input. The reason this works is that distillation recovers an approximation to the original model. By using a small number of samples and ensembling, the defender can mitigate the risk of sampling inputs for which the original and backdoored models disagree. This allows the defender to make a good prediction of what the original model would have done on the given input, thereby allowing the backdoor trigger to be detected.[6]
We can think of this strategy as a form of regularization. Because \(\varepsilon\) was small compared to 1/(VC dimension), the attacker had to choose a backdoored function that was very "strange", and so the defender was able to use distillation plus ensembling to obtain a similar function that was more "normal". However, other methods of regularization also work. For example, we also show (in Appendix A of the paper) that another strategy that works almost as well is to resample from a Boltzmann distribution centered on the given function.
Implications for deceptive alignment
In the case of deceptive alignment, our result initially appears to be a great success for the defender. If \(\varepsilon\) were large compared to 1/(VC dimension), then the two models would disagree frequently during ordinary model training (assuming a linear relationship between the number of parameters and training set size), causing the deceptive behavior to be trained away. Hence it is reasonable to assume that \(\varepsilon\) is small compared to 1/(VC dimension), which by our result implies that defense is statistically possible.
Unfortunately, though, our strategies for the defender seem unlikely to transfer well from our formal game to deceptive alignment. The "distillation plus ensembling" strategy works by using resampling to avoid the randomly-chosen trigger. But in the case of deceptive alignment, the defection trigger is not chosen randomly, but instead depends on the model's careful internal reasoning. Moreover, learning a new model from scratch seems likely to run into the same problems that gave rise to deceptive alignment in the first place. Thus this strategy appears to be exploiting the flaw in our analogy.
Similarly, other forms of regularization seem unlikely to transfer well to deceptive alignment. Indeed, a main worry when considering deceptive alignment is that it may be favored by many regularizers, e.g. because consequentialist cognitive strategies are deeper and more general than other strategies. This suggests modifying our formal game to allow the adversary to have more say over how the backdoor trigger is chosen.
Computational impossibility of dynamic backdoor detection
Our second main result concerns the version of the game in which the defender is required to run in polynomial time. Under certain cryptographic assumptions, we show (in Theorem 5.2) that the attacker can insert an undetectable backdoor into a polynomial size Boolean circuit.[7] The original function and the backdoored function only disagree on the backdoor trigger itself, and yet the backdoor is undetectable in the sense that a polynomial-time defender can only do negligibly better than chance in our formal game.
This result works by combining a puncturable pseudorandom function with an efficient indistinguishability obfuscator. Roughly speaking, puncturability of the pseudorandom function allows the backdoor to be inserted at a single point, and the efficient indistinguishability obfuscator allows this insertion to be obfuscated so that the defender cannot tell that it has been performed.[8]
Implications for deceptive alignment
This worst-case construction may initially seem irrelevant to deceptive alignment, since it is rather unlikely that something as precise as an indistinguishability-obfuscated puncturable pseudorandom function would arise out of ordinary model training. However, it is much more plausible for a trained neural network to be "punctured and obfuscated" in a more informal sense. Indeed, most trained neural networks remain largely obfuscated to humans attempting to understand their inner workings, despite the valiant attempts of mechanistic interpretability researchers. Hence we should arguably treat the theoretical possibility of obfuscation as a potential problem for detecting deceptive alignment in practice.
Fortunately, though, in the case of deceptive alignment, we have more information that we can potentially use, since we can observe not just the trained model, but also the entire training process. A similar situation arises with our theoretical construction, for which the attacker uses a secret key: if the defender had access to the secret key, then it would be easy for them to distinguish the original and backdoored functions. This suggests that, even in the presence of obfuscation, we may still be able to detect deceptive alignment by leveraging information about how the model was trained.
Conclusion
Our theoretical analysis of backdoors, together with related prior work, suggests that:
- Statically detecting whether a model is deceptively aligned is computationally infeasible under worst-case assumptions.
- Dynamically detecting when deceptive alignment is triggered (i.e., when a deceptively aligned model is run on a defection trigger), or modifying a model so that it is not deceptively aligned, may be possible in practice using regularization, depending on properties of the method of regularization used.
- Dynamically detecting when deceptive alignment is triggered is computationally infeasible under worst-case assumptions.
- Dynamically detecting when deceptive alignment is triggered can perhaps be made computationally feasible, even under worst-case assumptions, by leveraging information about how the model was trained.
In order to improve our understanding of deceptive alignment, we could study alternative versions of our backdoor detection game. In our version, we artificially constrain the attacker by requiring the backdoor trigger to be chosen randomly, but we could instead impose alternative constraints to break the symmetry between the original and backdoored functions. Some potential modifications include:
- We could require the original function to be learned from a dataset. (If we allow the attacker to alter a certain fraction of the dataset, then we recover the well-studied data poisoning setting.)
- We could require the backdoor trigger to satisfy some formal predicate that is expensive to check, but otherwise allow the attacker to choose the backdoor trigger.
- We could restrict the computational budget given to the attacker.
- We could require the computational trace of the attacker to be made accessible to the defender, as an analogy for observing the training process.
Some variants of this game may prove fruitful to study empirically as well as theoretically, as discussed in the post Concrete empirical research projects in mechanistic anomaly detection. Mechanistic anomaly detection is another informally-defined dynamic backdoor detection problem that attempts to generalize dynamic detection for deceptive alignment, which could also be modeled as a formal game in various ways.
Overall, we would be excited to see further work on such variants, as well as on open questions about our own formal game, especially the existence of "mechanistic" defenses (as discussed in Sections 6 and 7 of the paper).
Cross-postings for comments: Alignment Forum, LessWrong
The likelihood of deceptive alignment in realistic AI systems is discussed in the paper Scheming AIs: Will AIs fake alignment during training in order to get power?. ↩︎
The restriction to 0,1-valued functions can be thought of as reading from our model one bit at a time, perhaps ignoring bits that are unimportant such as differences in phrasing. This makes it possible to make use of concepts such as the VC dimension. We don't think this restriction makes a fundamental difference to the interpretation of our results. ↩︎
In the case of deceptive alignment, the robustly aligned model isn't chosen adversarially. However, we may not be able to make many assumptions about it, and so we allow the attacker to choose \(f\) in our game as a worst-case assumption. ↩︎
Again, allowing the attacker to choose the distribution \(\mathcal D\) is a worst-case assumption. ↩︎
The VC inequality for neural networks is notoriously weak, but to the extent that learning outperforms theoretical bounds in practice, this will be reflected in our defense algorithm, which uses learning. ↩︎
This strategy is essentially taken from the paper On Optimal Learning Under Targeted Data Poisoning (Theorem 3.1). ↩︎
Boolean circuits are essentially as expressive as neural networks. ↩︎
A private puncturable pseudorandom function might also suffice for this construction. ↩︎