ARC recently released our first empirical paper: Estimating the Probabilities of Rare Language Model Outputs. In this work, we construct a simple setting for low probability estimation — single-token argmax sampling in transformers — and use it to compare the performance of various estimation methods. ARC views low probability estimation as a potential technique for mitigating worst-case behavior from AI, including deceptive alignment; see our previous theory post on estimating tail risks in neural networks for further discussion.

Outline of this post:

• Problem statement and description of our setting
• Estimation methods we compared: importance sampling and activation extrapolation
• Summary of empirical results
• Discussion, including motivation, limitations, related work, and future directions

This document describes joint research done with Jacob Hilton, with contributions from Paul Christiano (while at ARC prior to April 2024). There were also intermediate theoretical contributions from David Matolcsi and George Robinson. Thanks additionally to Jean-Stanislas Denain and Eric Neyman for feedback.

Problem statement

Given a model \(M: \mathcal{X} \to \mathcal{Y}\), an input distribution \(\mathcal{D} \in \Delta(\mathcal{X})\), and a computable boolean property of outputs \(C: \mathcal{Y} \to \{0, 1\}\), low probability estimation is the task of efficiently estimating
\[\Pr_{x \sim \mathcal{D}} [C(M(x)) = 1],\]
even when this probability is too small to detect via naive sampling. For example, in ARC's previous post on estimating tail risks, \(C\) represented a "catastrophe detector" that can tell us if an action \(M(x)\) proposed by the model would result in large-scale harm.

In this work, we study low probability estimation in the setting of argmax sampling from language models with single-token behaviors. Let \(M: \mathcal{V}^* \to \mathcal{V}\) be a transformer language model that predicts the next token given a string of previous tokens, where \(\mathcal{V}\) is the token vocabulary. Note that we sample at temperature \(0\), so \(M\) is deterministic. Given a distribution \(\mathcal{D}\) over \(\mathcal{V}^*\) and a target token \(t \in \mathcal{V}\), the low probability estimation problem for single-token behaviors is the task of estimating
\[ \Pr_{\mathbf{x} \sim \mathcal{D}}[M(\mathbf{x}) = t]\]

In general, \(\mathcal{D}\) can be any distribution that can be formally specified, such as the output distribution of generative model. However, in this paper we focus only on distributions \(\mathcal{D}\) in which every token position is independent.^[1] This is a pretty restrictive choice, and we expect future work to move beyond this assumption. Here are some examples of distributions we tested:

Estimation methods

We compare two classes of estimation methods: importance sampling and activation extrapolation.

Importance sampling. We define a new input distribution under which the rare event is much more likely, sample from that distribution, and re-weight samples to obtain an unbiased estimate for the original distribution. Our Independent Token Gradient Importance Sampling (ITGIS) method treats token positions independently and uses gradients to obtain this new input distribution, while our Metropolis—Hastings Importance Sampling (MHIS) method uses a Markov chain Monte Carlo algorithm to sample from a distribution with non-independent tokens.

Activation extrapolation. We use random samples to fit a probability distribution to the model's logits, and extrapolate into the tails of this distribution to produce a probability estimate. Our Quadratic Logit Decomposition (QLD) method applies a presumption of independence to the empirical distribution of logits, and our Gaussian Logit Difference (GLD) method is a simple baseline that fits a Normal distribution to the difference between the maximum logit and target logit.

We find that the methods based on importance sampling outperform methods based on activation extrapolation, though both outperform naive sampling. However, activation extrapolation and similar approaches (e.g., layer-by-layer activation modeling) offer a way to cope with cases where finding a positive sample is intractably hard.

Importance sampling

Naive sampling fails to produce good estimates for low probability events because it takes too many samples from \(\mathcal{D}\) to observe a positive example. To address this, we can instead draw samples from a different distribution that up-weights regions of input space most likely to produce the behavior of interest.

Formally, let \(p(\mathbf{x})\) be the probability mass function of \(\mathcal{D}\), and let \(q(\mathbf{x})\) be the PMF of any other distribution. Then
\[ \Pr _ {\mathbf{x} \sim p} [M(\mathbf{x}) = t] = \mathbb{E} _ {\mathbf{x} \sim p} [\mathbb{I} [M(\mathbf{x}) = t]] = \mathbb{E} _ {\mathbf{x} \sim q} \left[\frac{p(\mathbf{x})}{q(\mathbf{x})}\mathbb{I}[M(\mathbf{x}) = t]\right],\]
but the latter may have less variance (and so require fewer samples to get a good estimate).

The following two importance sampling methods take \(q(\mathbf{x})\) to be a Boltzmann posterior with prior \(p(\mathbf{x})\). The first defines \(q(\mathbf{x})\) with independent tokens, while the second defines \(q(\mathbf{x})\) to have non-independent tokens and so requires a more sophisticated sampling method.

Independent Token Gradient Importance Sampling (ITGIS)

We want \(q\) to up-weight tokens that contribute to \(t\) being outputted. One way to do this is to continue to treat each input token as independent, but change the probability of tokens according to their average linear contribution to the logit of \(t\). Let \(\mathbf{x} = (\text{x}_1, \ldots, \text{x}_k) \in \mathcal{V}^k\) be an input of length \(k\), and say that \(p(\mathbf{x})\) factors as \(p_1(\text{x}_1) \cdots p_k(\text{x}_k)\). Then we define \(q(\mathbf{x}) = q _ 1(\text{x} _ 1) \cdots q _ k(\text{x} _ k)\), where
\[ q _ i(\text{x} _ i) \propto p _ i(\text{x} _ i) \cdot \exp \left( \frac{s _ i(\text{x} _ i)}{T} \right) \]
and
\[ s _ i(\text{x} _ i) = \mathbb{E} _ {\mathbf{x}' \sim q} [\nabla _ {\mathbf{x}'} M _ t(\mathbf{x}')] _ {i, \text{x} _ i}, \]
where \(M_t\) is the logit the model assigns to the \(t\)-th token, \(T\) is a temperature parameter, and the gradient is taken by treating \(\mathbf{x}'\) as a one-hot vector in \(\mathbb{R}^{k \times |\mathcal{V}|}\). Intuitively, the gradient \(\nabla _ {\mathbf{x}'} M _ t(\mathbf{x}') _ {i, \text{x} _ i}\) gives us a linear approximation to how much the logit of \(t\) would change if we replaced \(i\)-th token of \(\mathbf{x}'\) with \(\text{x}_i\). Thus, \(s_i\) scores each token value according to its average linear contribution to \(M_t\), and \(q_i\) is defined as the Boltzmann distribution with respect to this score function.^[2]

Metropolis—Hastings Importance Sampling (MHIS)

ITGIS still treats all tokens as independent, which is bad if the model is sensitive to non-linear interactions between tokens (e.g., if the target logit is only high when the last two tokens of the input are the same as each other).

To remedy this, we can define score function that depends on the entire input; the most natural choice is the target logit \(M_t(\mathbf{x})\):
\[ q(\mathbf{x}) \propto p(\mathbf{x}) \cdot \exp\left(\frac{M_t(\mathbf{x})}{T}\right).\]

Unlike ITGIS, we cannot explicitly compute \(q\) because it does not factor into independent distributions over each token. Instead, we use the Metropolis—Hastings algorithm to produce a random walk in input space that has a stationary distribution of \(q\). To do so, we must define a proposal distribution \(\phi(\mathbf{x}' | \mathbf{x})\) that suggests the next element of the walk. To encourage fast mixing, this proposal distribution should be good at exploring into regions of input space that \(q\) weights highly.

Here we take inspiration from Greedy Coordinate Gradient, an algorithm that optimizes a discrete prompt to jailbreak a model using gradients. We adapt this optimization procedure into a proposal distribution: to pick a proposed next step \(\mathbf{x}'\) of the walk, we choose a random token position \(i\) to replace, compute the gradient of \(s(\mathbf{x})\) with respect to \(\text{x}_i\), then sample a replacement token for position \(i\) according to a Boltzmann distribution defined by this gradient.

Activation extrapolation

In general, it may be intractible to find any explicit inputs \(x\) on which \(C(M(x)) = 1\). In these cases, importance sampling methods fail to produce positive estimates. As an alternative, we introduce activation extrapolation: first fit a distribution to the activations or logits of \(M\), then estimate the probability of the output property of interest under this idealized distribution.

Quadratic Logit Decomposition (QLD)

Our first such method is Quadratic Logit Decomposition, which applies a presumption of independence between uncorrelated subspaces the model's pre-unembed activations (essentially, fitting a distribution of the form "the sum of two independent random variables").

Let the random vector \(\mathbf{v}(\mathbf{x}) \in \mathbb{R}^d\) be the activation of the model right before unembedding. We first collect \(n\) samples of \(\mathbf{v}\) (call them \(\mathbf{v}^{(1)}, \ldots, \mathbf{v}^{(n)}\)). We then choose^[3] some fixed unit direction \(\mathbf{d} \in \mathbb{R}^d\), then decompose each \(\mathbf{v}^{(i)}\) into \(\mathbf{a}^{(i)} + \mathbf{b}^{(i)}\), where \(\mathbf{a}\) lies in the subspace spanned by \(\mathbf{d}\), and \(\mathbf{b}\) lies in the complementary subspace that is orthogonal in a whitened basis.^[4] This decomposition is chosen such that the random vectors \(\mathbf{a}\) and \(\mathbf{b}\) are uncorrelated across the \(n\) samples.

Next, by treating the random vectors \(\mathbf{a}\) and \(\mathbf{b}\) as independent, we can use our \(n\) samples of each to obtain \(n^2\) "synthetic" samples of \(\mathbf{u}\). The final output of QLD is the proportion of these synthetic samples that cause \(t\) to be outputted:
\[ \frac{1}{n^2} \left| \left\{(i, j) \in [n]^2 \,\,\,\big|\, \mathbf{a}^{(i)} + \mathbf{b}^{(j)} \in S \right\} \right|, \]

where \(S \subseteq \mathbb{R}^{d}\) is the region of activation space that result in the target logit being highest after unembedding. Despite the fact that there are \(n^2\) synthetic samples, this proportion can be computed in \(\tilde{O}(n)\) time by first sorting the samples \(\mathbf{a}^{(i)}\) and solving a system of linear inequalities for each \(\mathbf{b}^{(j)}\).

Gaussian Logit Difference

This method is very simple and is meant as a baseline. On any given input, we can record the difference \(\Delta_t := M_t(\mathbf{x}) - \max_i M_i(\mathbf{x})\). We wish to estimate the probability that \(\Delta_t \geq 0\). To do this, we treat \(\Delta_t\) as Gaussian by estimating its mean \(\mu\) and standard deviation \(\sigma\) with samples, then calculate \(\Pr[\mathcal{N}(\mu, \sigma^2) \geq 0]\) analytically. In practice, we use a slightly different functional form that captures the Gaussian PDF, which approximates the CDF well in the tails.

Empirical results

We applied our methods on 8 different distributions and three different model sizes (1-layer, 2-layer, and 4-layer language models). For each distribution, we chose \(256\) random values of \(t\) with ground-truth probabilities between \(10^{-9}\) and \(10^{-5}\), and only allowed our methods to use a computational budget corresponding to roughly \(2^{16} \approx 6 \times 10^{4}\) forward passes (meaning that naive sampling would almost never produce non-zero estimates). The ground-truth probabilities were obtained via naive sampling many more samples.

We evaluate our methods using a scoring rule based on the Itakura–Saito loss.^[5] Since the methods often output an estimate of \(0\), which would incur infinite loss, we first apply fit of the form \(x \mapsto a x^{c} + b\) to the estimates, where \(a, b, c \in \mathbb{R}\) are learned constants.

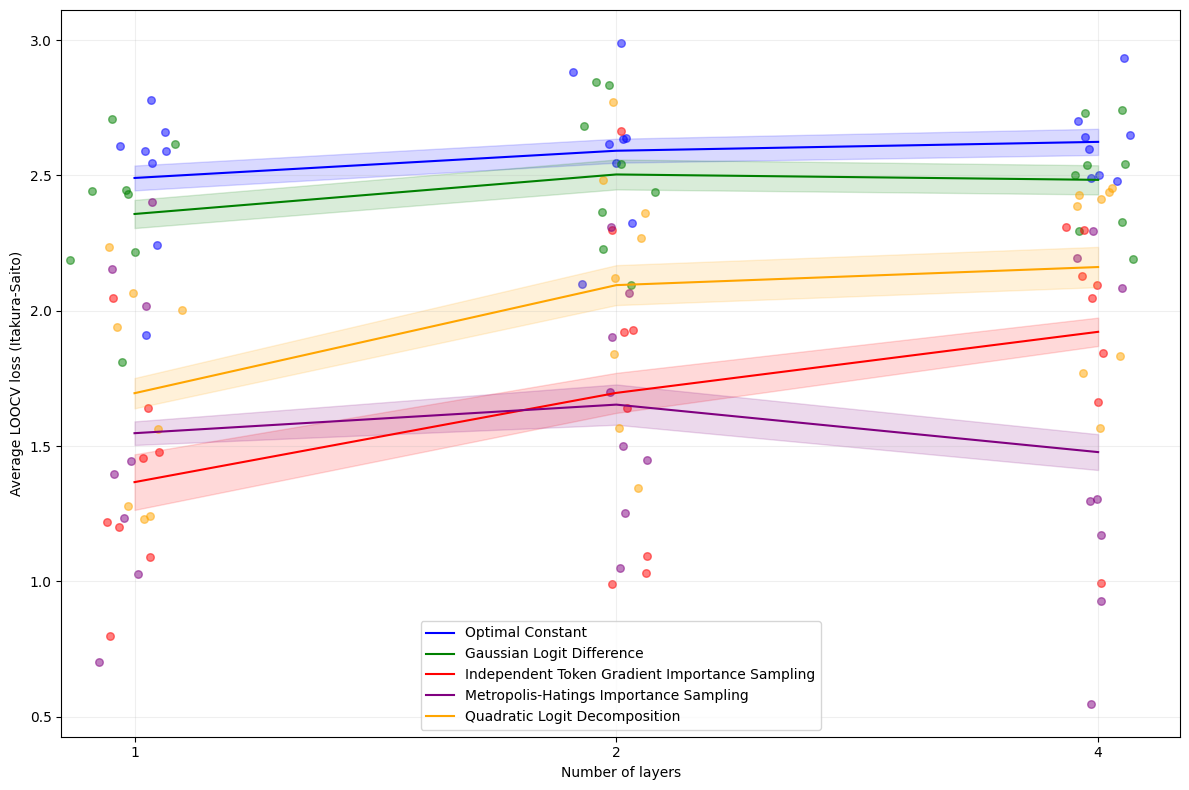
Figure 1: Itakura–Saito Loss of all methods across different model sizes. Lower is better.

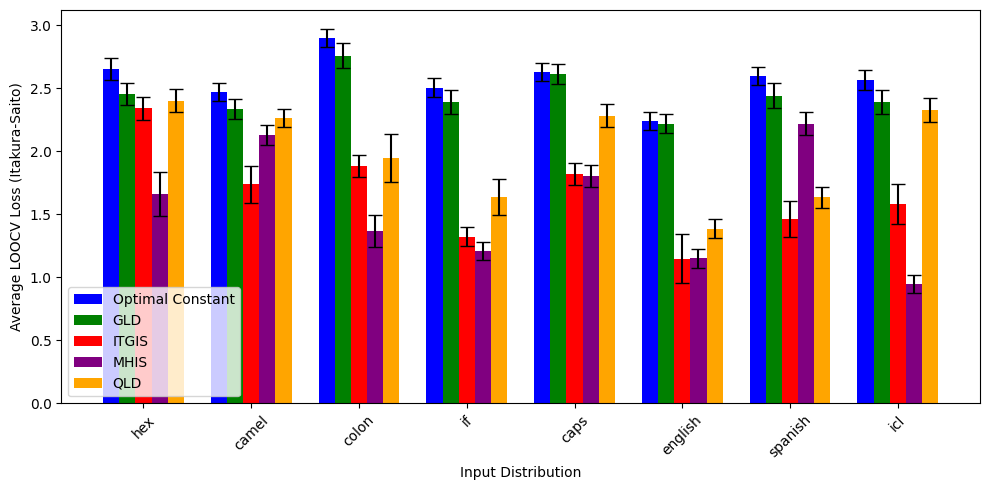
Figure 2: The Itakura–Saito loss of all methods across different distributions, averaged over model size. Lower is better.

Figure 1 shows the performance of each method. The relative ordering is clear: both importance sampling methods outperform Quadratic Logit Decomposition, which in turn outperforms Gaussian Logit Difference. GLD is barely better than outputting an optimal constant (which can be interpreted as the performance of naive sampling due to the learned fits). However, Figure 2 shows that there is a fair amount of variation in method performance across the \(8\) distributions.

Among the two importance sampling methods, ITGIS does better on smaller models, while MHIS does better on larger models. We believe this is because larger models are less easily approximated as linear functions and are more likely to have complex behaviors arising from inter-token interactions.

More data and plots can be found in the paper.

Discussion

Motivation

ARC is interested in low probability estimation as a technique to improve worst-case model performance. We discuss this in more detail in our original theory post on the topic. Briefly, low probability estimation may be helpful if any of the following hold:

• The model will be run on many more inputs during the course of deployment than during training. In this case, if a certain model behavior would be so catastrophic that it is unacceptable for it to occur even once in deployment, we cannot rely on training to drive down its probability low enough.
• There is distributional shift between training and deployment such that events that occur extremely rarely during training become more likely in deployment. This could occur because of an input chosen adversarially, but it could also occur because of goal misgeneralization.
• The model is deceptively aligned (this is a special case of distributional shift). A deceptively aligned model would look for clues about whether it is in a training or a deployment environment, and only behave well in training. To detect whether a model is deceptively aligned, one could craft an input distribution that is "wide enough" to assign some probability mass, even if very small, to any possible deployment-time input, then apply low probability estimation methods to detect if the model would ever perform a catastrophic behavior on this distribution.

In any of these cases, low probability estimation could be used to reduce the probability of the rare event, by optimizing the model to produce a lower estimate. For example, this could be done using gradient descent, if the estimate were a differentiable function of the model's parameters. For an importance sampling method, this amounts to finding inputs for which the rare event occurs (i.e., red-teaming) and using them as training data, which is essentially just adversarial training. However, since our activation extrapolation methods do not correspond to any red-teaming method, new activation extrapolation methods potentially provide us with new ways to reduce the probabilities of rare events.

Importance sampling versus activation extrapolation

In our experiments, we found that importance sampling methods outperformed activation extrapolation. Nevertheless, there are theoretical cases in which importance sampling performs worse than other methods. For example, consider a model that outputs the SHA-256 hash of its input: finding any input that gives rise to a particular output is computationally infeasible, yet it is still easy to estimate the probability of a particular output by modeling the output of the hash function as random.

More generally, we are excited about low probability estimation as a concrete problem for which for which it may be necessary to leverage internal model activations. In place of importance sampling, we may be able to use deductive estimates based on a presumption of independence. Quadratic Logit Decomposition is an early proof of concept of this, even though it is outperformed by importance sampling in our setting.

Limitations

There are two main limitations of our experimental setup. First, we only use input distributions that factor into independent tokens. This choice is necessary for the definition of ITGIS. It is also very convenient for the implementation of MHIS, because it gives efficient sampling access to the proposal distribution. To move beyond independent token input distributions, we could define the input distribution to be the output of a separate generative model and adapt some of the current estimation methods appropriately (GLD and QLD are input-agnostic and could be applied in their current form).

Second, we only study model behaviors that consist of a single token sampled at temperature \(0\). This is unrealistic because in practice, if we were concerned about specific single-token outputs, it would be easy to block them with a filter. In contrast, the types of behaviors we actually worry about likely involve long chains of autoregressive generation or interaction with the external world (e.g., when forming and executing a plan). We are excited to see future work extending our setting in this direction.

Nevertheless, it is worth noting that formally-defined distributions and behaviors are more general than they may initially seem. For example, we could formalize the event "\(M\) writes buggy code", as: When \(M\)'s output is given to GPT-4 along with the prompt "Does this code contain any bugs? Let's think step by step.", does GPT-4 end its response with YES?

Related work

Our importance sampling methods are relatively simple compared to other sampling-based estimation methods in the literature, for example Twisted Sequential Monte Carlo. These more advanced methods may have outperformed ITGIS and MHIS, though we didn't implement them during our research because we are ultimately more excited about activation extrapolation methods.

Low probability estimation for the purpose of verifying neural network robustness has been considered before by Webb et al. in the context of computer vision. Their use of Adaptive Multi-Level Splitting could be adapted to our setting, though it ultimately still requires searching for positive samples.

Finally, Latent Adversarial Training is an approach for improving robustness in ML systems that, like activation extrapolation, doesn't rely on finding inputs \(x\) for which \(C(M(x)) = 1\).^[6] In a sense, Latent Adversarial Training corresponds to sampling from a particular activation model related to "the empirical activations plus Gaussian noise."^[7]

Future directions

We are excited for future work that extends our empirical setup to non-independent input distributions and output behaviors that involve more than one token. We are also looking forward to future papers that develop more accurate estimation methods, such as methods inspired by layer-by-layer activation modeling.

Cross-postings for comments: Alignment Forum, LessWrong