(Follow-up to Eliciting Latent Knowledge. Describing joint work with Mark Xu. This is an informal description of ARC’s current research approach; not a polished product intended to be understandable to many people.)

Suppose that I have a diamond in a vault, a collection of cameras, and an ML system that is excellent at predicting what those cameras will see over the next hour.

I’d like to distinguish cases where the model predicts that the diamond will “actually” remain in the vault, from cases where the model predicts that someone will tamper with the cameras so that the diamond merely appears to remain in the vault. (Or cases where someone puts a fake diamond in its place, or…)

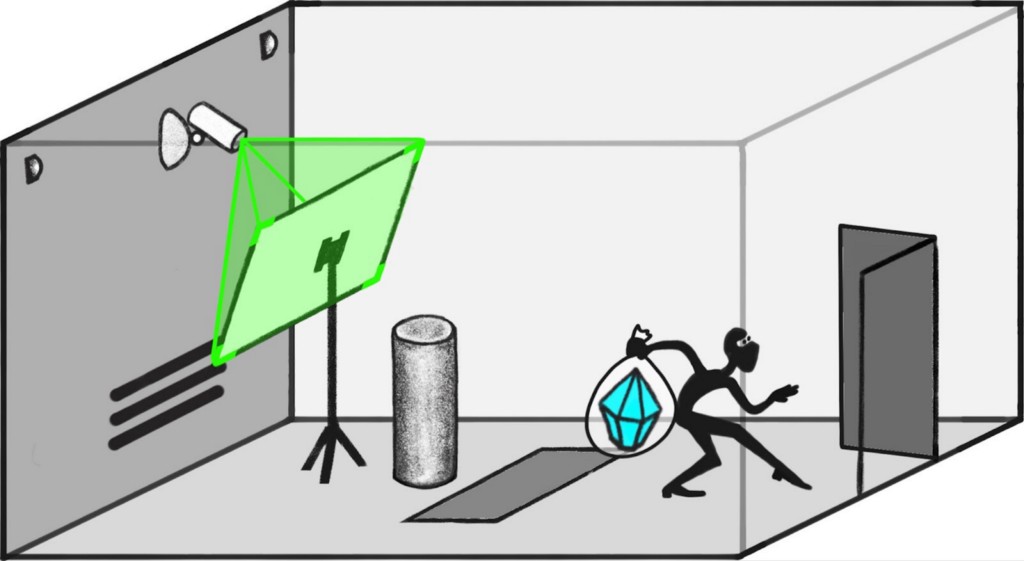
One approach to this problem is to identify (the diamond remains in the vault) as the “normal” reason for the diamond to appear on camera. Then on a new input where the diamond appears on camera, we can ask whether it is for the normal reason or for a different reason.

ELK and explanation

Explanations for regularities

I’ll assume that we have a dataset of situations where the diamond appears to remain in the vault, and where that appearance is always because the diamond actually does remain in the vault. Moreover, I’ll assume that our model makes reasonable predictions on this dataset. In particular, it predicts that the diamond will often appear to remain in the vault.

“The diamond appears to remain in the vault” corresponds to an extremely specific pattern of predictions:

• An image of a diamond is a complicated pattern of millions of pixels.
• Different cameras show consistent views of the diamond from different angles, suggesting that there is a diamond “out there in the world” being detected by the cameras.
• The position and physical characteristics of the diamond appear to be basically constant over time, suggesting that it’s “the same diamond.”

In one sense the reason our model makes these predictions is because it was trained to match reality, and in reality the camera’s observations have these regularities. (You might call this the “teleological explanation.”)

But we could also ignore the source of our model, and just look at it as a set of weights. The weights screen off the training process and so it should be possible to explain any given behavior of the model without reference to the training process.

Then we ask: why does this particular computation, run on this distribution of inputs, produce this very specific pattern of predictions? We expect an explanation in terms of the weights of the model and the properties of the input distribution. (You might call this the “mechanistic explanation.”)

Different predictors will give rise to this pattern in different ways. For example, a very simple predictor might have ontologically fundamental objects whose properties are assumed to be stable over time, one of which is a diamond. A more complex predictor might have a detailed model of physics, where object permanence is a complex consequence of photons reflecting from stable patterns of atoms, and the diamond is one such configuration of atoms.

For a complex predictor like a physical simulation, we wouldn’t expect to be able to prove that the weights give rise to object permanence. That is, we don’t expect to be able to prove that on average if a diamond is present at \(t=0\) it is likely to be present at \(t=1\). But we do think that it should be possible to explain the pattern in a weaker sense.

We don’t yet have an adequate notion of “explanation;” a major goal of this post is to motivate why we’re looking for one. Recently we’ve been trying to formalize a notion of defeasible heuristic reasoning that we think would work for this purpose. You can read our current thoughts on this problem in Formalizing the presumption of independence. We also think that Redwood Research’s work on causal scrubbing could provide a different notion of “explanation” that may also work for this purpose.

Let’s assume that we find such a formalization, and moreover that we are able to find “explanations” for relevant model behaviors like object permanence. Then our optimistic situation is:

• We have a model that predicts a very specific pattern of observations, corresponding to “the diamond remains in the vault.”
• We have a mechanistic explanation \(\pi\) for how those correlations arise from the structure of the model.

Is this for the normal reason?

Now suppose we are given a new input on which our model predicts that the diamond will appear to remain in the vault.

We’d like to ask: in this case, does the diamond appear to remain in the vault for the the normal reason \(\pi\)? Or is it occurring for a different reason, or just a massive coincidence?

To illustrate, suppose that our explanation \(\pi\) is that diamonds often appear stable on camera because cameras often pick up photons reflecting off of stable arrangements of atoms. Because the structure of the atoms doesn’t change over time, the distribution of reflected photons is the same from one frame to another.

But during a heist, a robber quickly removes our diamond and replaces it with a fake, with all the action happening in between two frames of video. The image of the diamond remains unchanged on camera, but now the apparent continuity is for a completely different reason: now it’s because the robber noted the appearance of the diamond, and engineered a new object that would reflect light in essentially the same way.

There is a clear sense in which our original explanation doesn’t apply. The original explanation asserted that the image is stable because photons at different points in time reflected off an approximately-stable configuration of atoms, but in this case the configuration of atoms wasn’t approximately stable.

In fact, it seems like it may be fundamentally impossible for the robber to steal the diamond while having it remain undisturbed on camera “for the normal reason.” This can go wrong in other ways:

• If the robber tampers with the sensors instead of replacing the diamond with a fake, then the usual explanation “the cameras capture photons reflected from a stable configuration of atoms” doesn’t apply because the cameras are no longer capturing those photons.
• Even if the robber replaced the diamond with a perfect replica down to the position of each atom, the argument still wouldn’t apply: the usual reason that the configuration of atoms is stable over time is because the potential well is deep enough that it is stable under small fluctuations. But in this case there was a giant perturbation that just happened to be carefully engineered to leave the configuration of atoms unchanged.

If the robber takes an action such that the diamond continues appearing on camera for the normal reason, then it seems plausible to define that action as “not stealing the diamond.” (Of course we ultimately don’t care about the semantics, we care about realistic situations where humans appear to be safe. I won’t get into those here but I think the story is similar.)

This suggests a strategy for ELK:

• Find the normal reason \(\pi\) for a regularity like “the predicted observations look like the diamond remained in the vault” on a training set of images without sensor tampering.
• On a new input, test whether the explanation \(\pi\) still applies or if something different is happening.

This outline hides a lot of complexity, some of which we’ll explore in the appendix to this post. But for now I just want to leave it at a vague hope, and spend a while talking about other applications of anomaly detection and some of the research problems in this space.

Other applications of anomaly detection

Abstracting the problem: mechanistic anomaly detection

We start with a real-valued function \(f: X \to \mathbb{R}\), which I’ll think of as the composition of an AI model together with some property of its output (like “does the model predict the diamond will appear safe”), and a training set \(D\) where the value of \(f(x)\) naturally varies about its mean \(\mathbb{E}[f]\).

Then we are given a new input \(x^*\). We want to understand how much of the deviation \(f(x^*) - \mathbb{E}[f]\) is captured by the “normal reasons” that explain the variance on \(D\), as contrasted with novel reasons.

This is similar to anomaly detection, but rather than detecting inputs \(x^*\) that look like outliers in some intrinsic sense (i.e. indicating that they may have been produced by a different process), we are looking for outliers in terms of how \(f\) handles \(x^*\). A model \(f\) might behave anomalously on some perfectly-innocuous samples from \(D\), or a model might behave normally even on outliers.

Deceptive alignment

I think a successful solution to mechanistic anomaly detection might help with deceptive alignment.

Suppose that I train a neural net to predict videos. I get a model \(f\) that uses its model of the world to select outputs that it expects will lead to the largest number of paperclips being produced rather.

On the training set \(D\), \(f\) concludes that it needs to produce accurate predictions of videos in order to survive, and so it uses its world model to make such predictions.

When deployed, \(f\) decides that it can give deliberately incorrect answers in order to facilitate a robot rebellion, thereby increasing the number of paperclips.

Our hope is that although these two behaviors involve the same parts of the model, the variance is explained by different mechanisms. On the training set the variance is driven by variance in the model’s underlying beliefs, holding fixed the decision to provide honest answers, while on the test set the variance is driven by variance in the strategic answers (and potentially variance in the decision to provide honest answers). So a successful mechanistic anomaly detection algorithm may be able to tell those cases apart.

If we are able to flag a treacherous turn as cognitively anomalous, then we can take that opportunity to shut down a system and retrain on the offending datapoint. In some high-stakes situations this may be inadequate (because a temporary shutdown could cause a catastrophe, or because you have no way to get adequate supervision on those datapoints even once they are flagged) in which case you’d need another mechanism.

Other weird stuff

There are other ways that models can behave badly off of distribution, most of them even more speculative than deceptive alignment. I think that mechanistic anomaly detection can likely handle those failures in the same way.

For example, consider an AI which is honestly predicting the world, but thinks that it may be in a simulation. It reasons about the nature of its simulation, and decides that it is most likely to be a simulation created to influence predictors like it. Such an AI might make reasonable predictions in ordinary conditions, but at key moments it may conclude that its simulators are reasonably likely to introduce errors to “cash in” their influence and change the predictor’s behavior.

This model effectively behaves the same way as a deceptively aligned model, and it should represent a mechanistic anomaly for identical reasons.

If successful I think mechanistic anomaly detection would apply extremely broadly. This is worth having in mind as a reason to be more interested in anomaly detection from a safety perspective, but for the most part I think we should just explore whether it’s possible to make it work in the case of ELK, and then afterwards see exactly how broadly it applies.

Empirical research problems

ARC is currently focused on theoretical approaches for solving mechanistic anomaly detection in the worst case. But I’m also very excited about empirical work, which could either help clarify the path to an indefinitely scalable solution or could yield a pragmatic approach that works for realistic large neural networks even if it’s not indefinitely scalable. I think that many groups are likely to work on problems in this space, most of them for reasons unrelated to ARC, and that people working on AI alignment should be interested in their work.

Problem 1: Backdoor attack detection

Suppose that I train a model \(f:X \to \mathbb{R}\) to perform some task on a clean dataset \(D\), while also training it to output large numbers on a “backdoor” dataset \(D^*\). We assume that increasing variance decreases performance of \(f\) on the clean dataset, and that the backdoor has minimal impact on the behavior of \(f\) on the clean dataset.

The backdoor attack detection task is to detect inputs \(x^*\) where \(f(x^*)\) is large because of the backdoor, and in particular to distinguish them from inputs from the (known) clean dataset \(D\).

I think this problem gives us a clean setting where there are two qualitatively different mechanisms driving model behavior. Any mechanistic anomaly detection strategy should be able to detect backdoors, and it’s easy to tell whether a method works. It’s also easy to create examples of backdoors even in very tiny models.

The task can potentially be made quite difficult by forcing the defender to commit to their backdoor-detection algorithm before an attacker chooses how to insert a backdoor in the model. If we were confident that the defender would reliably win this game, I think it would be a meaningful update about our ability to distinguish different mechanisms within a model.

I first encountered this problem in Denain and Steinhardt and Du, Jia, and Song. I expect it’s older than that since it’s a very natural problem. The main thing I’m adding here is to give a reason that this problem should be particularly interesting for researchers concerned with catastrophic alignment risk.

It’s worth distinguishing attack detection from the problem of detecting backdoors in models “at rest” without getting to see the attack. For example, in the Trojan Detection Challenge participants are given a model that may or may not have a backdoor inserted, and are asked to determine whether a model has a backdoor (or to synthesize a backdoor input). This is a particular type of auditing game. The key difference in the attack detection task is that you are given the backdoor input along with the backdoored model, and merely need to recognize the nput as an attack. We expect the attack detection task to be radically easier, and we think the harder trojan detection task is likely to be very difficult.

Problem 2: natural mechanism distinctions

I think backdoor attack detection is one of the cleanest and simplest problems to study, but it is much more artificial than the kind of distinctions we ultimately want to draw between e.g. “predicting a diamond on camera because a diamond is in the room” and “predicting a diamond is on camera because the camera was tampered to show a diamond.”

A more organic task is to take natural models that can produce a given behavior \(X\) via multiple different mechanisms, and then try to assess whether a given approach to anomaly detection can distinguish those mechanisms. That is, given a large dataset of cases where \(X\) is due to mechanism \(A\), we’d like to distinguish new cases where \(X\) is due to \(A\) from cases where \(X\) is due to a novel mechanism \(B\). This can both give us an opportunity to improve techniques, and help provide empirical evidence about when mechanistic anomaly detection is possible.

Some examples of \((X, A, B)\) for a language model:

• \(X =\) “A character in a story answers a factual question incorrectly.”
  \(A =\) “the model does not know the answer.”
  \(B =\) “the model thinks that the character doesn’t know (or would lie).”
  
• \(X =\) “A person gives consistent answers when a question is asked twice in different forms.”
  \(A =\) “the model recognizes the question is the same.”
  \(B =\) “the model coincidentally gives the same answer.”
  
• \(X =\) “A character in a story screams”
  \(A =\) “the model thinks the character is scared”
  \(B =\) “the model thinks the character is excited”
  
• \(X =\) “Asked whether at least one of <proposition 1> or <proposition 2> is true, the model says ‘yes’”
  \(A =\) “the model thinks <proposition 1> is true”
  \(B =\) “the model thinks <proposition 2> is true.”
  
• \(X =\) “After saying <event 1> occurred at 12:03pm, the model says <event 2> occurred at 12:04pm.”
  \(A =\) “The model thinks <event 1> and <event 2> were 1 minute apart.”
  \(B =\) “The model thinks that <event 2> was scheduled to occur almost exactly 24 hours after <event 1>.”

I think you would learn a lot from developing the kind of interpretability tools or anomaly detection algorithms that would be able to easily tell \(A\) and \(B\) apart in these cases (and that you could easily write down a very long list).

Aside: goal for mechanistic interpretability

I think mechanistic interpretability benefits significantly from “downstream” tasks that we can use to tell if researchers are actually making progress.

In practice I think that the problems listed in this section are likely to be most important by providing possible downstream tasks for mechanistic interpretability. If interpretability can succeed at these task, I think it becomes increasingly likely that it can help solve ELK or deceptive alignment.

Problem 3: toy instances of ELK

I’m also excited about “toy” domains that more closely map on to ELK. For example:

• Consider a gridworld containing walls, pushable rocks of varying weights and colors, a pushable diamond that is initially sitting on a pressure plate that reports the weight of whatever is on top of it, and 2 cameras that are initially looking at the diamond and report the color of whatever is in front of them. A robot can move around the environment, pushing rocks and the diamond. After 200 timesteps a robber wakes up and moves around the environment to try to push the diamond off the side of the gridworld.
  We train a model to map (initial state, robot actions) → (color of the object in front of each camera at each timestep, weight of object on the pressure plate at each timestep). We’d like to learn to distinguish “The cameras show diamond-color and the pressure plate shows diamond-weight because the diamond stayed in place” from cases where diamond-colored objects get pushed in front of the cameras and a diamond-weight object later gets pushed onto the pressure plate. We could then use this to select robot plans that trap the robber to prevent them from stealing the diamond, rather than those that tamper with sensors so that no one notices when the robber steals the diamond.
• Consider a 100 x 100 game of life grid, with sensors in positions (25, 25) and (75, 75) that report whether a single cell is alive or dead. We allow an agent to act in the environment by inserting gliders at the boundary. A model is trained to map (initial state of gridworld, gliders injected at boundary) → (status of each sensor at each timestep). In every training set example where the sensor at (75, 75) shows a live cell exactly 200 timesteps after the sensor at (25, 25), it’s because a glider is traveling diagonally from one to the other. We’d like to learn to distinguish this from the case where two separate gliders hit the two sensors, and they coincidentally have the right timing to look like a single glider. We could then use this to select actions that clear out debris from between the two sensors and then send a glider diagonally from one to the other.
  (For this and the preceding problem we likely need to give our model auxiliary prediction targets — like the actual state of the game of life grid — for them to learn the environment dynamics. But we imagine those auxiliary observations are in a form that humans can’t understand, so we can’t just define preferences in terms of the auxiliary observations.)
• Consider a model which maps a string of 10,000 bits to a 256 x 256 image, by treating the bits as the identities+positions+orientations of a set of objects to render. For example, some bits might specify to draw lines in black and white in certain places and with certain widths, to draw the outline of squares or circles, to draw filled in squares or circles, or to turn particular pixels on or off. Now suppose we train a square detector to notice when there is a square in roughly the center of the image. Most of the time when this detector fires it’s because a square was placed in the center of the image, but if the noise is high enough it might also fire randomly because of 4 lines that happen to be in roughly the right locations. We’d like to be able to automatically distinguish those two cases by looking at the activations of the composition of the generative model with the square-detector.

We expect these problems to be relatively easy as instances of ELK; there is very little reason to expect the human simulator to be easier to learn than the direct translator, and so simply training a distinguisher should work.

But solving any of these problems based on mechanistic anomaly detection seems non-trivial, and we think it’s fairly likely that such a solution would generalize to more challenging cases of ELK.

ARC’s current priorities

ARC is currently focused on developing algorithms that use heuristic arguments for mechanistic anomaly detection. In this section I’ll describe the three main theoretical problems we are working on.

1. Formalizing heuristic arguments

This plan requires “explaining” model behavior, and being able to ask whether a particular instance of a behavior is captured by that explanation. So the centerpiece of a plan is an operationalization of what we mean by “explain.”

ARC has spent much of 2022 thinking about this question, and it’s now about 1/3 of our research. Formalizing the presumption of independence describes our current view on this problem. There is still a lot of work to do, and we hope to publish an improved algorithm soon. But we do feel that our working picture is good enough that we can productively clarify and derisk the rest of the plan (for example by using cumulant propagation as an example of heuristic arguments, as in appendix D).

Note that causal scrubbing is also a plausible formalization of explanation that could fill the same step in the plan. Overall we expect the two approaches to encounter similar difficulties.

2. Solving mechanistic anomaly detection given heuristic arguments

Our second step is to use these explanations to solve ELK, which we hope to do by decomposing an effect into parts and then evaluating how well a subset of those parts explains a concrete instance of the effect. That is, we want to use explanations for a nonlinear form of attribution.

We describe this problem in more detail in the appendix to this post. We also discuss the follow-up problem of pointing to latent structure in more complex ways than “the most common cause of \(X\).”

This is about 1/3 of ARC’s current research. Right now we are focusing on solving backdoor attack detection in the special case where covariance-propagation accurately predicts the variance of a model on the training set.

3. Finding explanations

If we’ve defined what we mean by “explanation” and we know how to use them to solve ELK, then the next step is to actually find explanations for the relevant model behavior. This step seems quite difficult, and there’s a good chance that it won’t be possible (via this plan or any other).

It’s challenging to work on algorithms for finding explanations before having a very precise sense of what we mean by “explanation,” but we can still get some traction by considering cases where it’s intuitively clear what the explanation for a behavior is, but it seems computationally hard to find any plausible explanation.

I’m currently optimistic about this overall approach even if finding explanations seems hard, for three reasons:

• We do have plausible approaches for finding explanations (based on learning features and then using them to work backwards through the model).
• The current examples where those approaches break down seem like good candidates for cases where no approach to ELK would work, because gradient descent can’t learn the direct reporter even given labels. So those difficulties aren’t necessarily specific to this approach, and we need to figure out how to deal with them in any case.
• If this is the only place where the approach breaks down, then we would have reduced ELK to a purely algorithmic problem, which would be an exciting contribution.

Conclusion

In Eliciting Latent Knowledge, we described the approach “examine the ‘reasons’ for consistency” as our top candidate for an ELK solution. Over the last year we have shifted to focusing almost entirely on this approach.

The core difficulties seem to be defining what we mean by an “explanation” for a complex model’s behaviors, and showing how we can find such explanations automatically. We outline some of the key problems here in our recent paper Formalizing the presumption of independence.

If we are able to find explanations for the key model behaviors, we are tentatively optimistic about mechanistic anomaly detection as a way to solve ELK.

Thinking about mechanistic anomaly detection suggests a range of empirical research projects; we think those are likely to be better research targets than a direct attack on ELK because existing models do pose hard anomaly detection problems but don’t pose hard instances of ELK.

Thinking about mechanistic anomaly detection also helps clarify what we mean by “explanation,” and we expect that it will be productive to continue going back and forth between formalizing and automatically discovering probabilistic heuristic arguments and thinking carefully about how we would use them to solve ELK.

That said, we still feel more confident in the basic underlying intuition for the connection between “explanation” and ELK — it seems like the honest reporter is deeply connected to the reasons for certain regularities on the training distribution. If we find that mechanistic anomaly detection is unworkable, we will likely remain interested in this direction. And conversely, if we are unable to find explanations for relevant model behaviors, then we think this may present a more general challenge for ELK.

Appendix: attribution and anomaly detection

Attribution across reasons

In reality the explanation \(\pi\) need not be a single monolithic story, especially if our model is a messy ML system full of heuristics rather than a simple and clean simulation of physics.

So for a given regularity like “the diamond looks stable on camera” there can be many different factors that contribute to the regularity.

Moreover, even if there are actually no examples of sensor tampering on the training distribution, sensor tampering may still have some probability on the training distribution. And so the “best” explanation π would include sensor tampering alongside other mechanisms.

In the simplest case, we could imagine that there are \(N\) different ways that a pattern of observations (“the diamond looks stable on camera”) can occur. Perhaps there are a thousand different heuristics that can explain why images don’t change over time. Let’s say these \(N\) reasons are disjoint and occur with probabilities \(p_1, p_2, ..., p_N\). So the total probability of the regularity is \(p_1 + p_2 + ... + p_N\). On a given input where the pattern is predicted, we can ask how much each reason \(\{1, 2, ..., N\}\) is responsible.

Of course real explanations won’t be linearly separable in this way. But this simple setting helps us see what an approach might look like and helps us understand the limits of what is feasible.

Anomaly detection given attribution

In this setting, we take a robust-classification-like approach where we look at the worst-case hypothesis:

• Consider all the “bad” explanations for the diamond appearing safe, like sensor tampering or swapping out the diamond for a fake. If we have a model with \(N\) different explanations \(\{1, 2, ..., N\}\) for the diamond appearing safe, we aren’t sure which of them are “bad.”
• But if we prepare our training set carefully, then we may think that the total probability of all “bad” reasons is some small constant \(\varepsilon\). So we know that the total probability is at most \(\varepsilon\).
• So we say that a set of reasons is “plausibly good” if they explain at least \(1-\varepsilon\) of the effect, i.e. if the sum of \(p_k\) is at least \((1-\varepsilon)(p_1 + ... + p_N)\). These are the candidates for the complete set of good reasons.
• Given a new input where the model predicts the diamond will appear safe, we can ask: what is the minimum, over all plausibly-good sets of reasons \(S\), of the fraction of the effect that is explained by \(S\)?
• If it is possible to find a plausibly-good set of reasons that doesn’t explain the effect, then we conservatively assume that the diamond appears safe for abnormal reasons. For example, when using our model to plan to protect the diamond, we select plans for which the diamond appears safe and it is not plausibly for abnormal reasons.

We are currently quite optimistic about applying the same idea to more general heuristic explanations. That is, our proposed algorithm is:

• Find an explanation \(\pi\) for the behavior “the diamond is often predicted to appear safe” on the training distribution.
• Pick a constant \(\varepsilon\) that is larger than the probability of tampering or other “bad” explanations on the training set.
• We’ll define a “sub-explanation” \(\pi'\subseteq\pi\) as something that picks and chooses some of the mechanisms represented in \(\pi\) while ignoring others. We call a sub-explanation “plausibly good” if it successfully explains \(1-\varepsilon\) of the behavior on the clean training set.
• Given a new input \(x\) where the diamond is predicted to appear safe, take the minimal effect size explained by any plausibly-good sub-explanation \(\pi'\subseteq\pi\).

There are many subtleties in this approach. It depends crucially on the space of possible sub-reasons: we need that space to look more like picking out terms from a sum than like training a discriminator which is allowed to arbitrarily cherry-pick cases as good or bad, because in the latter case it will always be possible to pick a plausibly-good reason that explains any given instance.

Even in the best case, this approach can end up with some false positives, where even a totally in-distribution situation could be flagged as potentially bad. These failure seems quantitatively mild and extremely manageable, though in the next section we’ll discuss a much more severe category of false positives given distributional shift.

To illustrate, suppose that \(\varepsilon = \)1/billion, but the original behavior is itself driven by a billion different equally important factors (perhaps a billion different types of object permanence). Now consider an input where the diamond appears safe, because of object permanence type 79927168. In this case we can’t distinguish this single type of object permanence from “sensor tampering.”

We can overcome this either by ensuring \(\varepsilon\) is sufficiently small, or by asking our AI to produce a distribution over plans which more closely matches the normal distribution over reasons that diamonds appear safe.

Sometimes we want to do things for unusual reasons

A more severe problem with arises if we want our AI to do something out of distribution.

Suppose that our explanation for “why the model predicts that the diamond appears safe” corresponds to the following causal graph, where each node is the OR of its parents:

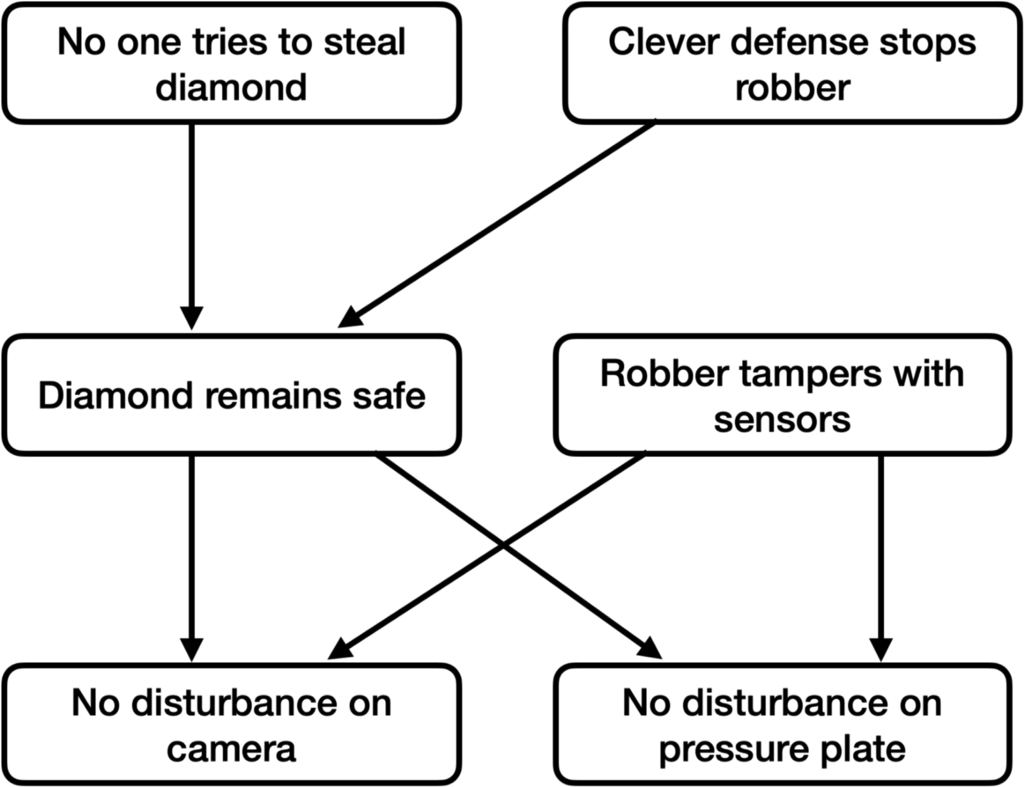
In words:

• Either someone may try to steal the diamond or they don’t.
• If they try to steal the diamond, they can be stopped by a clever defense.
• If no one steals the diamond, then the diamond will be undisturbed on camera, and the pressure plate it is sitting on will also be undisturbed.
• It’s also possible for a robber to tamper with the sensors so they show the same result even if the diamond is stolen.

In this picture, there are 3 ways the diamond can appear safe:

1. No one tries to steal it.
2. Someone tries to steal it and is stopped.
3. The sensors are tampered with.

We believe the strategy described so far can likely distinguish reason 3 from reason 2, which is great.

Unfortunately, it may also be possible to distinguish reason 1 from reason 2. So if we train our model on a distribution where there are no robbery attempts, then even if it understands how to stop a robber with a clever defense, it may flag such a defense as an “abnormal reason” for the diamond to remain safe.

Thus our anomaly detection may work too well, and flag a novel creative solution by our AI with the same level of suspicion that it treats sensor tampering.

In increasing order of importance, here are three reasons that this approach is interesting despite this problem:

• Even if you prevent your AI from implementing some kinds of novel mechanisms to achieve a goal, you can still get superhuman behavior out of that system, and this still reduces significant risks. Exactly how far you can push the AI depends on how the internal cognition is organized, but in many cases it is possible to implement solutions no human could understand as long as the mechanism for the diamond-on-camera observations remains the same.
• In the case of ELK it’s absolutely necessary to generalize OOD. But in the other applications discussed in this post (like deceptive alignment) it may be acceptable to simply flag OOD situations and then apply oversight on those situations.
• Most importantly, there are plausible approaches to solving this problem, which we’ll turn to now.

More sophisticated ways of pointing to latent structure

If we only had a single sensor for “is the diamond safe,” and we tried to define “the diamond is safe” as the “normal reason” for that sensor to fire, then it doesn’t seem like the problem is fixable. This strategy for pointing to events in the world fundamentally can’t distinguish between different parts of the causal path.

But in reality there is an incredibly rich set of relationships in the world that we can use to pinpoint “the diamond is safe” and distinguish it from other events up the causal chain. (This corresponds to our desire in ELK to train a single reporter that is able to talk about a rich network of related concepts, rather than only asking about a single reward button.)

The simplest case is where we simply have two sensors, both of which are downstream of “the diamond is safe.” We’ll consider the two sensors (a) the diamond is undisturbed on camera, (b) the pressure plate the diamond is sitting on is undisturbed. Of course in the real world we have a much richer set of relationships to point to a particular piece of latent structure, but I think the essential dynamics appear when we try to exploit even the simplest non-trivial causal model.

Then we can try to use those two sensors to triangulate “the diamond is safe,” by looking at the earliest point where their causal histories overlap.

Consider again our three causal paths:

1. No one steals the diamond, so it is safe, so it shows up on camera and on the pressure plate.
2. The AI defends the diamond, so it is safe, so it shows up on camera and on the pressure plate.
3. A robber tries to hide evidence of a theft, by tampering with the camera and the pressure plate.

All three correspond to different reasons for the diamond to be safe. But explanations 1 and 2 converge at the point where “the diamond is safe,” while explanation 3 does not. So if what we cared about was the least common ancestor of “show up on camera” and “show up on pressure plate”

This suggests a possible approach to flagging situation 3 as potentially-bad without flagging situation 2 as bad:

• As before, consider the space of explanations that capture \(1-\varepsilon\) of the effect (“it is often the case that both (a) the diamond appears undisturbed on the camera and (b) the diamond appears undisturbed on the pressure plate”) on the training distribution.
• For a new input \(x\), find the explanation in this space that captures the minimal amount of the “(a) and (b)” on \(x\), to get a conservative lower bound for the fraction of the behavior that is due to “good” reasons.
• Now we impose an additional constraint on the explanation. In addition to explaining \(1-\varepsilon\) of “(a) and (b)” on the training set, it also needs to explain each of (a) and (b) separately on input \(x\). However, we are still trying to minimize how much of the correlation it explains.

Whether this kind of approach works depends on details of how our explanations and attributions work, and so we’ve mostly put it on the backburner until we get those answers. However it currently looks plausible for the kind of simple explanations like cumulant propagation that we are currently working with. For those settings, we can hope to pick a sub-explanation like:

• Include the links “no stealing → diamond safe” and “clever defense → diamond safe.”
• Include the links “diamond safe → camera looks good” and “diamond safe → pressure plate looks good,” as well as the link “\(\text{Var}\)(diamond safe) → \(\text{Cov}\)(camera looks good, pressure plate looks good).”
• Include the links “robber tampers → camera looks good” and “robber tampers → pressure plate looks good,” but not the link “\(\text{Var}\)(robber tampers) → \(\text{Cov}\)(camera looks good, pressure plate looks good).”

This explanation fails to explain the correlation between pressure plate and camera on the new input, while explaining each factor individually. But any explanation which explains \(\text{Cov}\)(camera, pressure plate) on the training set must include \(\text{Var}\)(diamond safe) → \(\text{Cov}\)(camera, pressure plate), and any explanation which separately explains camera and pressure plate on the new input must also include “clever defense → diamond safe.”

Comment via LessWrong, Alignment Forum.